О звуке простыми словами42Производители Hi-Fi.
Истории и интервью111Репортажи с заводов51Репортажи с Hi-Fi выставок62"Сделай сам"42Готовые проекты Аудиомании42Пресса об Аудиомании52Видео488Фотогалерея101Интересное о звуке817Новости мира Hi-Fi2806Музыкальные и кинообзоры646Глоссарий
Фильтры. Отсекая лишнее. Журнал "Автозвук"
Профессиональный рецепт Огюста Родена наилучшим образом подходит для нашей темы. А тема была давно обещана читателям. Вновь разобраться с электрическими фильтрами во всех формах, в которых они применяются в нашей узкой отрасли....взять глыбу мрамора и отсечь от нее всё лишнее...
Огюст Роден
Любой фильтр, в сущности, делает со спектром сигнала то же, что Роден с мрамором. Но в отличие от творчества скульптора замысел принадлежит не фильтру, а нам с вами.
Нам с вами по понятным причинам больше всего знакома одна сфера применения фильтров — разделение спектра звуковых сигналов для последующего воспроизведения их динамическими головками (нередко мы говорим «динамиками», но сегодня материал серьёзный, поэтому к терминам будем тоже подходить со всей строгостью). Но эта область использования фильтров, наверное, всё же не основная и совершенно точно, что не первая в историческом плане. Не будем забывать, что электроника когда-то называлась радиоэлектроникой, и первоначальной её задачей было обслуживание нужд радиопередачи и радиоприёма. И даже в те детские годы радио, когда сигналы сплошного спектра не передавались, а радиовещание ещё называлось радиотелеграфией, возникла потребность повышения помехозащищённости канала, и решена эта задача была за счёт использования фильтров в приёмных устройствах. На передающей стороне фильтры применялись для ограничения спектра модулированного сигнала, чем также удалось повысить надёжность передачи. В конце концов, краеугольный камень всей радиотехники тех времён, резонансный контур — не что иное, как частный случай полосового фильтра. Поэтому можно сказать, что вся радиотехника началась с фильтра.
Конечно, первые фильтры были пассивными, состояли они из катушек и конденсаторов, а с помощью резисторов удавалось получить нормированные характеристики. Но все они обладали общим недостатком — их характеристики зависели от импеданса той цепи, которая стоит за ними, то есть цепи нагрузки. В простейших случаях импеданс нагрузки можно было поддерживать достаточно высоким, чтобы этим влиянием можно было пренебречь, в других случаях взаимодействие фильтра и нагрузки приходилось учитывать (между прочим, расчёты зачастую велись даже без логарифмической линейки, просто в столбик). Избавиться от влияния импеданса нагрузки, этого проклятия пассивных фильтров, удалось с появлением активных фильтров.
Изначально предполагалось посвятить этот материал целиком и полностью пассивным фильтрам, их в практике инсталляторов приходится рассчитывать и изготавливать своими силами несравнимо чаще, чем активные. Но логика потребовала, чтобы мы всё же начали с активных. Как ни странно, потому что они проще, что бы ни казалось при первом взгляде на приводимые иллюстрации.
Хочу быть понятым верно: сведения об активных фильтрах не призваны служить исключительно руководством по их изготовлению, такая надобность появляется далеко не всегда. Гораздо чаще возникает нужда понять, как работают уже имеющиеся фильтры (главным образом — в составе усилителей) и почему они не всегда работают так, как нам бы хотелось. И здесь, действительно, может прийти мысль о ручной работе.
Принципиальные схемы активных фильтров
В простейшем случае активный фильтр представляет собой пассивный фильтр, нагруженный на элемент с единичным коэффициентом передачи и высоким входным импедансом — либо на эмиттерный повторитель, либо на операционный усилитель, работающий в режиме повторителя, то есть с единичным усилением. (Можно реализовать и катодный повторитель на лампе, но ламп я, с вашего позволения, касаться не буду, если кому интересно — обратитесь к соответствующей литературе). По идее, не возбраняется таким способом построить активный фильтр любого порядка. Поскольку токи во входных цепях повторителя очень малы, то, казалось бы, элементы фильтра могут быть выбраны очень компактными. Все ли? Представьте себе, что нагрузкой фильтра является резистор 100 Ом, вы хотите сделать фильтр НЧ первого порядка, состоящий из единственной катушки, на частоту 100 Гц. Каков должен быть номинал катушки? Ответ: 159 мГн. Какая уж тут компактность. И главное, что омическое сопротивление такой катушки может оказаться вполне сравнимым с нагрузкой (100 Ом). Поэтому о катушках индуктивности в схемах активных фильтров пришлось забыть, другого выхода просто не было.
Для фильтров первого порядка (рис. 1) я приведу два варианта схемной реализации активных фильтров — с ОУ и с эмиттерным повторителем на транзисторе n-p-n типа, а вы уж сами при случае выберете, с чем вам проще будет работать. Почему n-p-n? Потому, что их больше, и потому, что при прочих равных условиях в производстве они получаются несколько «лучше». Моделирование проводилось для транзистора КТ315Г — единственного, наверное, полупроводникового прибора, цена на который до последнего времени была точно такая же, как и четверть века назад — 40 копеек. Фактически вы можете использовать любой n-p-n транзистор, коэффициент усиления которого (h21э) не намного ниже 100.
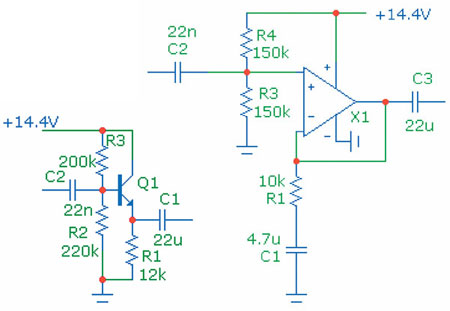
Рис. 1. Фильтры ВЧ первого порядка
Резистор в цепи эмиттера (R1 на рис. 1) задаёт ток коллектора, для большинства транзисторов его рекомендуют выбирать примерно равным 1 мА или немного меньше. Частоту среза фильтра определяет ёмкость входного конденсатора C2 и общее сопротивление параллельно включённых резисторов R2 и R3. В нашем случае это сопротивление составляет 105 кОм. Надо только следить, чтобы оно было значительно меньше, нежели сопротивление в цепи эмиттера (R1), умноженное на показатель h21э — в нашем случае это примерно 1200 кОм (в действительности при разбросе значений h21э от 50 до 250 — от 600 кОм до 4 МОм). Выходной конденсатор добавлен, что называется, «для порядка» — если нагрузкой фильтра будет входной каскад усилителя, там, как правило, уже стоит конденсатор для развязки входа по постоянному напряжению.
В схеме фильтра на ОУ здесь (как и в последующем) использована модель TL082C, поскольку этот операционный усилитель очень часто применяется для построения фильтров. Впрочем, можно брать едва ли не любой ОУ из тех, что нормально работают с однополярным питанием, предпочтительнее с входом на полевых транзисторах. Здесь также частота среза определяется соотношением ёмкости входного конденсатора C2 и сопротивлением параллельно включённых резисторов R3, R4. (Почему параллельно включённых? Потому, что с точки зрения переменного тока плюс питания и минус — одно и то же.) Соотношение резисторов R3, R4 определяет среднюю точку, если они будут немного различаться, это не трагедия, это лишь означает, что сигнал максимальной амплитуды начнёт ограничиваться с одной стороны несколько раньше. Фильтр рассчитан на частоту среза 100 Гц. Чтобы её понизить, надо увеличить либо номинал резисторов R3, R4, либо емкость C2. То есть номинал изменяется обратно пропорционально первой степени частоты.
В схемах фильтра НЧ (рис. 2) на пару деталей больше, поскольку входной делитель напряжения не используется как элемент частотно-зависимой цепи и добавляется разделительная ёмкость. Для понижения частоты среза фильтра надо увеличивать входной резистор (R5).
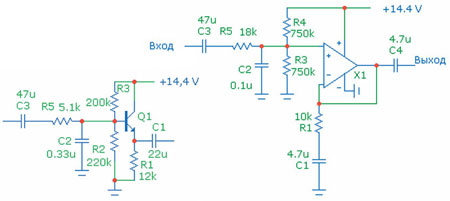
Рис. 2. Фильтры НЧ первого порядка
Разделительная ёмкость имеет нешуточный номинал, так что без электролита обойтись будет трудно (хотя можно ограничиться плёночным конденсатором 4,7 мкФ). Следует учитывать, что разделительная ёмкость совместно с C2 образуют делитель, и чем она меньше, тем выше ослабление сигнала. Как следствие, несколько смещается и частота среза. В некоторых случаях можно обойтись без разделительного конденсатора — если, к примеру, источником является выход другого каскада фильтра. А вообще стремление избавиться от громоздких разделительных конденсаторов и явилось, наверное, основной причиной перехода от однополярного питания к двухполярному.
На рис. 3 и 4 показаны частотные характеристики фильтров ВЧ и НЧ, схемы которых мы только что рассмотрели.
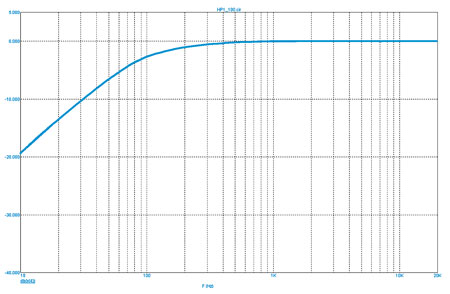
Рис. 3. Характеристики фильтров ВЧ первого порядка
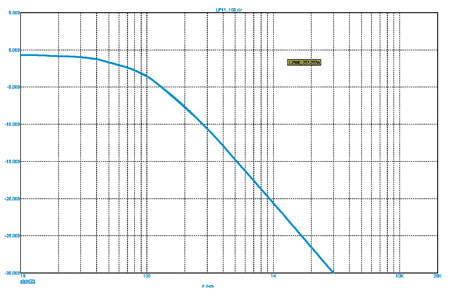
Рис. 4. Характеристики фильтров НЧ первого порядка
Весьма вероятно, что у вас уже возникли два вопроса. Первый: а что это мы так плотно занялись изучением фильтров первого порядка, когда для сабвуферов они не годятся вовсе, да и для разделения полос фронтальной акустики, если верить высказываниям автора, они применимы, мягко говоря, не часто? И второй: а почему автор не упомянул ни Баттерворта, ни его однофамильцев — Линквица, Бесселя, Чебышева, в конце концов? На первый вопрос я пока отвечать не буду, чуть позже вам всё станет ясно. Сразу перехожу ко второму. Баттервортом со товарищи были определены характеристики фильтров от второго порядка и выше, а частотная и фазовая характеристика фильтров первого порядка всегда одна и та же.
Итак, фильтры второго порядка, с номинальной крутизной спада 12 дБ/окт. Такие фильтры повсеместно делаются с использованием ОУ. Можно, конечно, обойтись и транзисторами, но для того, чтобы схема работала точно, приходится учитывать много всего, и в результате простота оказывается чисто мнимой. Известно энное количество вариантов схемной реализации таких фильтров. Я даже не скажу какое, поскольку любое перечисление всегда может оказаться неполным. Да и нам оно мало что даст, поскольку по-настоящему углубляться в теорию активных фильтров нам вряд ли имеет смысл. Тем более что в построении фильтров усилителей участвуют по большей части лишь две схемные реализации, можно даже сказать, что полторы. Начнём с той, которая «целая». Это так называемый фильтр Саллена — Ки (Sallen — Key).
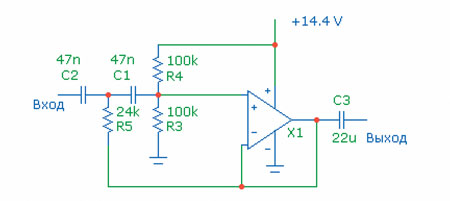
Рис. 5. Фильтр ВЧ второго порядка
Здесь, как и всегда, частота среза определяется номиналами конденсаторов и резисторов, в данном случае — C1, C2, R3, R4, R5. Обратите внимание, для фильтра Баттерворта (ну наконец-то!) номинал резистора в цепи обратной связи (R5) должен быть вдвое меньше номинала резистора, включённого в «землю». Как обычно, в «землю» получаются включенными резисторы R3 и R4 параллельно, и суммарный номинал их 50 кОм.
Теперь несколько слов как бы в сторону. Если у вас фильтр не перестраиваемый, проблем с подбором резисторов не будет. Но если вам надо плавно менять частоту среза фильтра, нужно одновременно изменять два резистора (у нас их три, но в усилителях питание двухполярное, и там один резистор R3, номинала такого же, как наши два R3, R4, включённые параллельно). Специально для таких целей выпускаются сдвоенные переменные резисторы разного номинала, но они и дороже, и не так их много. Кроме того, можно разработать фильтр с очень близкими характеристиками, но у которого оба резистора будут одинаковыми, а ёмкости C1 и C2 — разными. Но это хлопотно. А теперь давайте посмотрим, что будет, если взять фильтр, рассчитанный на среднюю частоту (330 Гц) и начать менять лишь один резистор — тот, который в «землю». (Рис. 6).
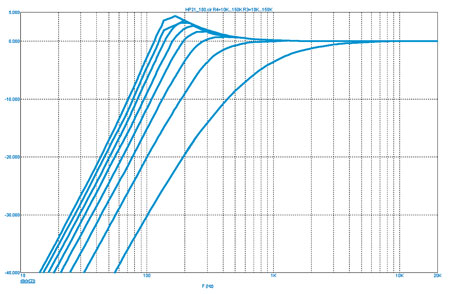
Рис. 6. Перестройка фильтра ВЧ
Согласитесь, нечто подобное мы многократно видели на графиках в тестах усилителей.
Схема фильтра НЧ похожа на зеркальное отображение фильтра ВЧ: в обратной связи стоит конденсатор, а в горизонтальной полке буквы «Т» — резисторы. (Рис. 7).
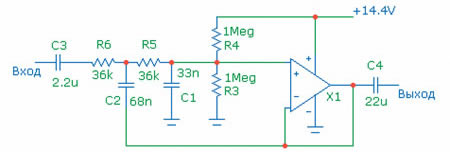
Рис. 7. Фильтр НЧ второго порядка
Как и в случае с фильтром НЧ первого порядка, добавляется разделительный конденсатор (C3). Величина резисторов в цепи создания локальной «земли» (R3, R4) влияет на величину затухания, вносимого фильтром. При указанном на схеме номинале аттенюация около 1,3 дБ, думаю, с этим можно мириться. Как всегда, частота среза обратно пропорциональна номиналу резисторов (R5, R6). Для фильтра Баттерворта номинал конденсатора в обратной связи (C2) должен быть вдвое больше, чем ёмкость C1. Поскольку номинал резисторов R5, R6 один и тот же, для плавной перестройки частоты среза подходит почти любой сдвоенный подстроечный резистор — именно поэтому во многих усилителях характеристики фильтров НЧ более стабильны, нежели характеристики фильтров ВЧ.
На рис. 8 показаны амплитудно-частотные характеристики фильтров второго порядка.
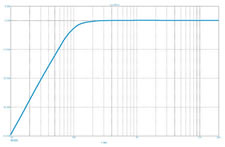
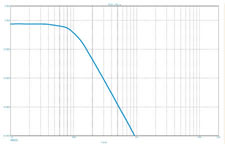
Рис. 8. Характеристики фильтров второго порядка
Вот теперь можно вернуться к тому вопросу, который остался без ответа. Схему фильтра первого порядка мы «проходили» потому, что активные фильтры создаются в основном путём каскадирования базовых звеньев. Так что последовательное соединение фильтров первого и второго порядка даст третий порядок, цепочка из двух фильтров второго порядка даст четвёртый и так далее. Поэтому я приведу лишь два варианта схем: фильтр ВЧ третьего порядка и фильтр НЧ — четвёртого. Тип характеристики — Баттерворт, частота среза — те же 100 Гц. (Рис. 9).
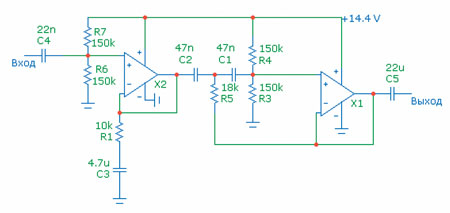
Рис. 9. Фильтр ВЧ третьего порядка
Предвижу вопрос: отчего вдруг изменились номиналы резисторов R3, R4, R5? А отчего бы им не измениться? Если в каждой «половинке» схемы уровню -3 дБ соответствовала частота 100 Гц, значит, совместное действие обеих частей схемы приведёт к тому, что спад на частоте 100 Гц составит уже 6 дБ. А мы так не договаривались. Так что самое привести методику выбора номиналов — пока только для фильтров Баттерворта.
1. По известной частоте среза фильтра задаться одним из характерных номиналов (R или C) и вычислить второй номинал, используя зависимость:
Fc = 1/(2?pRC) (1.1)
Поскольку ассортимент номиналов конденсаторов, как правило, более узкий, разумнее всего задаться базовым значением ёмкости C (в фарадах), а по нему определить базовое значение R (Ом). Но если у вас, к примеру, есть пара конденсаторов 22 nF и несколько штук на 47 nF, никто не мешает вам брать и те, и эти — но в разных частях фильтра, если он составной.
2. Для фильтра первого порядка формула (1.1) даёт сразу значение резистора. (В нашем конкретном случае получаем 72,4 кОм, округляем до ближайшего стандартного значения, получаем 75 кОм.) Для базового фильтра второго порядка вы точно так же определяете стартовое значение R, но для того, чтобы получить действительные значения резисторов, надо будет воспользоваться таблицей. Тогда номинал резистора в цепи обратной связи определится как
Rp = KpR (1.2)
а номинал резистора, идущего в «землю», будет равен
Rs = KsR (1.3)
| Порядок фильтра | Kp | Ks |
| 2 | 0,7070 | 1,414 |
| 3 | 0,5000 | 2,000 |
| 4 (1) | 0,3827 | 2,613 |
| 4 (2) | 0,9240 | 1,082 |
Единичкой и двойкой в скобках обозначены строки, относящиеся к первому и второму каскадам фильтра четвёртого порядка. Можете проверить: произведение двух коэффициентов в одной строке равно единице — это, действительно, обратные величины. Впрочем, мы договорились в теорию фильтров не лезть.
Расчёт номиналов определяющих компонентов фильтра НЧ осуществляется сходным образом и по той же таблице. С той только разницей, что в общем случае вам придётся танцевать от удобного номинала резистора, а номиналы конденсаторов подбирать по таблице. Конденсатор в цепи обратной связи определится как
Cp = KsC, (1.4)
а конденсатор, соединяющий вход ОУ с «землёй», как
Cs = KpC (1.5)
Пользуясь вновь приобретёнными знаниями, рисуем фильтр НЧ четвёртого порядка, который уже вполне можно применить для работы с сабвуфером (рис. 10). На схеме я на этот раз привожу расчётные значения емкостей, без округления до стандартного номинала. Это чтобы вы могли себя проверить при желании.
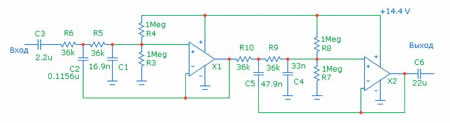
Рис. 10. Фильтр НЧ четвёртого порядка
Я до сих пор ни слова не сказал о фазовых характеристиках, и правильно сделал — вопрос этот отдельный, отдельно им и займёмся. В следующий раз, вы же поняли, мы только начинаем...
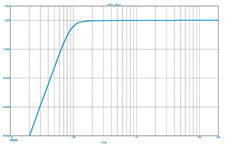
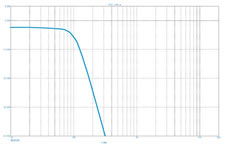
Рис. 11. Характеристики фильтров третьего и четвёртого порядка
Подготовлено по материалам журнала "Автозвук", апрель 2009 г. www.avtozvuk.com
Вот теперь, когда у нас накопилось некоторое количество материала, можно заняться фазой. Надо с самого начала сказать, что давным-давно понятие фазы ввели для обслуживания нужд электротехники.
Когда сигнал представляет собой чистый синус (хотя степень чистоты бывает разная) фиксированной частоты, то вполне естественно представить его в виде вращающегося вектора, определяемого, как известно, амплитудой (модулем) и фазой (аргументом). Для звукового сигнала, в котором синусы присутствуют лишь в виде разложения, понятие фазы уже не столь наглядно. Однако не менее полезно — хотя бы потому, что звуковые волны от разных источников складываются векторно. А теперь посмотрим, как выглядят фазочастотные характеристики (ФЧХ) фильтров до четвёртого порядка включительно. Нумерация рисунков будет сохраняться сквозная, с прошлого выпуска.
Начинаем, стало быть, с рис. 12 и 13.
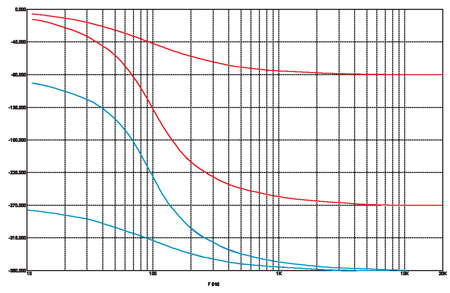
рис. 12
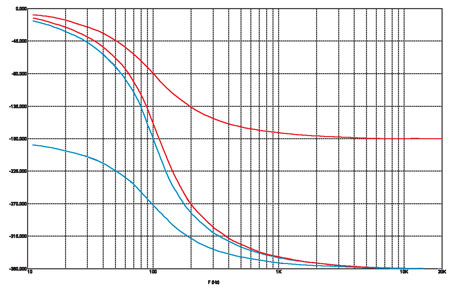
рис. 13
Сразу можно подметить любопытные закономерности.
1. Любой фильтр «крутит» фазу на угол, кратный ?/4, точнее говоря, на величину (n?)/4, где n — порядок фильтра.
2. ФЧХ фильтра НЧ всегда начинается от 0 градусов.
3. ФЧХ фильтра ВЧ всегда приходит на 360 градусов.
Последний пункт можно уточнить: «точка назначения» ФЧХ фильтра верхних частот кратна 360 градусам; если порядок фильтра выше четвёртого, то с ростом частоты фаза фильтра ВЧ будет стремиться к 720 градусам, то есть к 4? ?, если выше восьмого — к 6? и т. д. Но для нас это уже чистая математика, имеющая к практике весьма отдалённое отношение.
Из совместного рассмотрения перечисленных трёх пунктов нетрудно заключить, что ФЧХ фильтров ВЧ и НЧ совпадают лишь для чётвёртого, восьмого и т.д. порядков, а справедливость этого утверждения для фильтров четвёртого порядка наглядно подтверждает и график на рис. 13. Впрочем, из этого факта не следует, что фильтр четвёртого порядка «самый лучший», как, кстати, не следует и обратного. И вообще, выводы пока делать рано.
Фазовые характеристики фильтров не зависят от способа реализации — активные они или пассивные, и даже от физической природы фильтра. Поэтому мы не будем специально заострять внимание на ФЧХ пассивных фильтров, они по большей части ничем не отличаются от тех, что мы уже видели. Кстати говоря, фильтры относятся к числу так называемых минимально-фазовых цепей — их амплитудно-частотные и фазочастотные характеристики жёстко взаимосвязаны. К числу неминимально-фазовых звеньев относится, к примеру, линия задержки.
Совершенно очевидно (при наличии графиков), что чем выше порядок фильтра, тем его ФЧХ падает круче. А крутизну любой функции характеризуют чем? Её производной. Производная ФЧХ по частоте имеет специальное название — групповое время задержки (ГВЗ). Фазу надо брать в радианах, а частоту — не колебательную (в герцах), а угловую, в радианах в секунду. Тогда производная получит размерность времени, что объясняет (правда, частично) её название. Характеристики ГВЗ у однотипных фильтров ВЧ и НЧ ничем не отличаются. Вот так выглядят графики ГВЗ для фильтров Баттерворта с первого порядка по четвёртый (рис. 14).
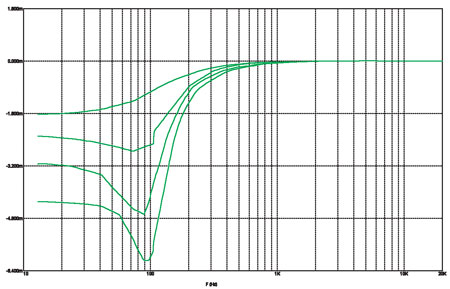
рис. 14
Тут разница между фильтрами разных порядков кажется особенно заметной. Максимальное (по амплитуде) значение ГВЗ для фильтра четвёртого порядка примерно вчетверо больше, чем у фильтра первого порядка и вдвое больше — чем у фильтра второго. Встречаются высказывания, что по этому параметру фильтр четвёртого порядка как раз вчетверо хуже, чем фильтр первого. Для фильтра ВЧ — возможно. Но для фильтра НЧ минусы высокого ГВЗ не столь существенны в сравнении с плюсами высокой крутизны спада АЧХ.
Для дальнейшего изложения нам полезно будет представлять себе, как выглядит ФЧХ «по воздуху» электродинамической головки, то есть как зависит фаза излучения от частоты.
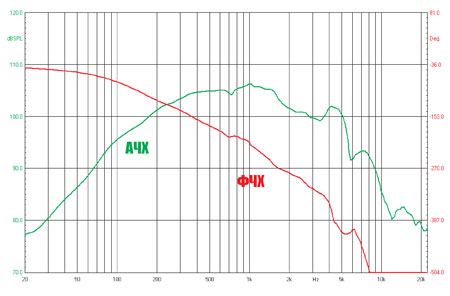
рис. 15
Примечательная картинка (рис. 15): на первый взгляд как у фильтра, но, с другой стороны, это вовсе и не фильтр — фаза всё время падает, причём с растущей крутизной. Не буду напускать лишнюю таинственность: так выглядит ФЧХ линии задержки. Люди опытные скажут: понятное дело, задержка обусловлена пробегом звуковой волны от излучателя до микрофона. И ошибутся опытные люди: микрофон у меня был установлен по фланцу головки; если даже брать в расчёт положение так называемого центра излучения, то это может вызвать погрешность 3 — 4 см (для данной конкретной головки). А тут, если прикинуть, задержка почти на полметра. А, собственно, почему её (задержки) не должно быть? Вот представьте себе на выходе усилителя такой сигнал: ничего-ничего, и вдруг синус — как ему и положено, из начала координат и с максимальной крутизной. (Мне, например, и представлять ничего не надо, у меня на одном из измерительных CD такое записано, мы по этому сигналу полярность проверяем.) Понятно, ток через звуковую катушку потечёт не сразу, у неё ещё какая-то индуктивность есть. Но это мелочи. Главное, что звуковое давление — это объёмная скорость, то есть диффузору надо сперва разогнаться, и только потом появится звук. Для величины задержки, наверное, можно вывести формулу, наверняка там будут фигурировать масса «подвижки», силовой фактор и, возможно, омическое сопротивление катушки. Кстати, подобные результаты я получал на разном оборудовании: как на аналоговом фазометре Bruel & Kjaer, так и на цифровых комплексах MLSSA и Clio. Точно знаю, что у среднечастотников задержка меньше, чем у басовиков, а у пищалок меньше, чем у тех и этих. Как ни удивительно, но в литературе я ссылок на подобные результаты не встречал.
Зачем я привёл этот поучительный график? А затем, что если дело действительно обстоит именно так, как мне видится, то многие рассуждения о свойствах фильтров теряют практический смысл. Хотя я их всё же изложу, а вы уже сами решите, все ли из них стоит принимать на вооружение.
Схемы пассивных фильтров
Думаю, мало кто удивится, если я заявлю, что схемных реализаций пассивных фильтров существует куда меньше, чем фильтров активных. Я бы сказал, что их примерно две с половиной. То есть если эллиптические фильтры выводить в отдельный класс схем, получится три, если этого не делать — то две. Причём в 90% случаев в акустике используются так называемые параллельные фильтры. Поэтому мы начнём не с них.
Последовательные фильтры, в отличие от параллельных, не существуют «по частям» — тут фильтр НЧ, а там фильтр ВЧ. А значит, вы не сможете подключить их к разным усилителям. К тому же по своим характеристикам это фильтры первого порядка. А между прочим, ещё вездесущий господин Смолл обосновал, что фильтры первого порядка для акустических применений непригодны, что бы там ни говорили ортодоксальные аудиофилы (с одной стороны) и сторонники всемерного удешевления акустической продукции (с другой). Однако у последовательных фильтров есть один плюс: сумма выходных напряжений у них всегда равна единице. Вот как выглядит схема двухполосного последовательного фильтра (рис. 16).
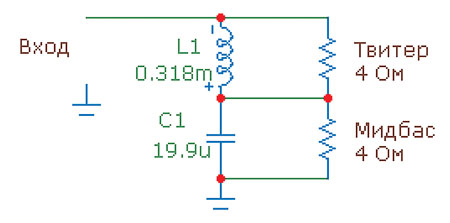
рис. 16
В данном случае номиналы соответствуют частоте среза 2000 Гц. Нетрудно понять, что сумма напряжений на нагрузках всегда в точности равна входному напряжению. Эта особенность последовательного фильтра используется при «подготовке» сигналов для их дальнейшей обработки процессором (в частности, в Dolby Pro Logic). На следующем графике вы видите АЧХ фильтра (рис. 17).
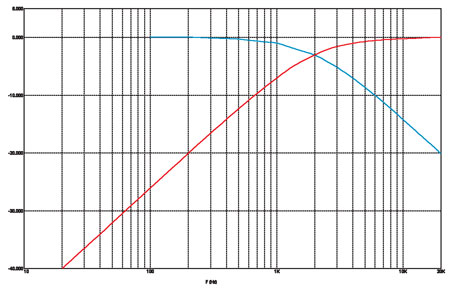
рис. 17
Можете поверить, что графики ФЧХ и ГВЗ у него точно такие же, как и у любого фильтра первого порядка. Науке известен и трёхполосный последовательный фильтр. Схема его на рис. 18.
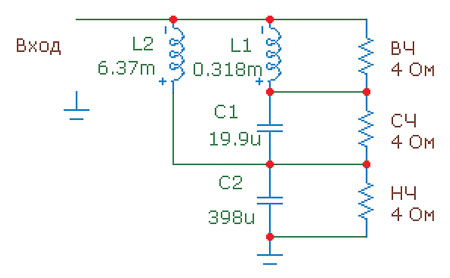
рис. 18
Приведенные на схеме номиналы соответствуют той же частоте раздела (2000 Гц) между твитером (ВЧ) и среднечастотником и частоте 100 Гц — раздела между СЧ и НЧ-головками. Понятно, что трёхполосный последовательный фильтр обладает тем же свойством: сумма напряжений на его выходе в точности равна напряжению на входе. На следующем рисунке (рис. 19), где приведен набор характеристик этого фильтра, вы можете увидеть, что крутизна спада фильтра пищалки в диапазоне 50 — 200 Гц выше, чем 6 дБ/окт., поскольку его полоса тут накладывается не только на полосу СЧ, но и на полосу НЧ головки. Вот уж чего не умеют делать параллельные фильтры — у них перехлёст полос неизбежно преподносит сюрпризы, и всегда — нерадостные.
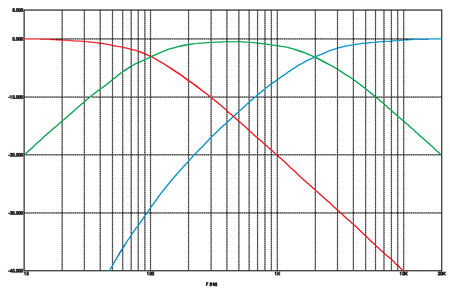
рис. 19
Параметры последовательного фильтра рассчитываются в точности так же, как и номиналы фильтров первого порядка. Зависимость всё та же (см. формулу 1.1). Удобнее всего ввести так называемую постоянную времени, через частоту среза фильтра она выражается как TO = 1/(2?Fc).
Тогда
C = TO/RL (2.1), а
L = TO*RL (2.2).
(Здесь RL — импеданс нагрузки, в данном случае 4 Ом).
Если, как во втором случае, у вас трёхполосный фильтр, то частот раздела будет две и постоянных времени тоже две.
Наверное, самые технически подкованные из вас уже заметили, что я слегка «передёрнул» карты и заменил реальный импеданс нагрузки (то есть динамика) омическим «эквивалентом» 4 Ом. В действительности, конечно, никакой он не эквивалент. На самом деле даже принудительно заторможенная звуковая катушка с точки зрения измерителя импеданса выглядит как последовательно соединённые активное и индуктивное сопротивление. А когда катушка обладает подвижностью, индуктивность возрастает на высокой частоте, а вблизи частоты резонанса головки у неё как бы возрастает омическое сопротивление, случается, и в десять раз, и больше. Программ, которые умеют учитывать такие особенности реальной головки, очень немного, мне лично известно три. Но мы никоим образом не ставили своей целью научиться работать, скажем, в программной среде Linearx. У нас задача иная — разобраться с основными особенностями фильтров. Поэтому будем по старинке имитировать присутствие головки резистивным эквивалентом, и конкретно — номиналом 4 Ом. Если в вашем случае нагрузка имеет другой импеданс, то и все входящие в схему пассивного фильтра импедансы должны быть пропорционально изменены. То есть индуктивности — пропорционально, а ёмкости — обратно пропорционально сопротивлению нагрузки.
(Прочтя это в черновике, главный редактор сказал: «Ты что, последовательные фильтры — это Клондайк, давай копнём как-нибудь». Согласен. Клондайк. Пришлось обещать, что в одном из грядущих номеров отдельно и специально копнём.)
Получившие наиболее широкое распространение параллельные фильтры называют ещё «лестничными». Думаю, всем будет ясно, откуда взялось это название после того, как вы взглянете на обобщённую схему фильтра (рис. 20).
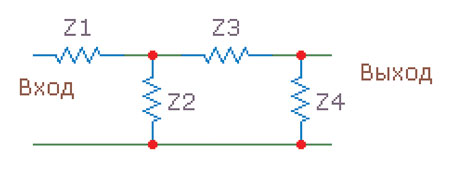
рис. 20
Чтобы получить фильтр НЧ четвёртого порядка, надо все горизонтальные «планки» в этой схеме заменить индуктивностями, а все вертикальные — емкостями. Соответственно, для построения фильтра ВЧ нужно сделать всё наоборот. Фильтры более низких порядков получаются путём отбрасывания одного или более элементов, начиная с последнего. Фильтры более высокого порядка получают аналогичным способом, только наращиванием числа элементов. Но мы с вами договоримся: выше четвёртого порядка фильтров для нас не существует. Как мы увидим позже, одновременно с ростом крутизны фильтра углубляются и их недостатки, поэтому такая договорённость не является чем-то крамольным. Для полноты изложения надо бы сказать ещё вот что. Существует альтернативный вариант построения пассивных фильтров, где первым элементом всегда ставится резистор, а не реактивный элемент. Такие схемы применяют, когда требуется нормировать входной импеданс фильтра (например, операционные усилители «не любят» нагрузку менее 50 Ом). Но в нашем случае лишний резистор — это неоправданные потери мощности, поэтому «наши» фильтры начинаются реактивностью. Если, конечно, не требуется специально снизить уровень сигнала.
Самый сложный по устройству полосовой фильтр получается, если в обобщённой схеме каждый горизонтальный элемент заменить последовательным соединением ёмкости и индуктивности (в любой последовательности), а каждый вертикальный элемент должен быть заменён параллельно включёнными — также ёмкостью и индуктивностью. Наверное, я всё-таки приведу такую вот «страшную» схему (рис. 21).
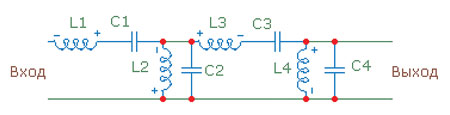
рис. 21
Есть ещё одна маленькая хитрость. Если вам понадобится несимметричный «бандпасс» (полосовой фильтр), у которого, скажем, фильтр ВЧ имеет четвёртый порядок, а фильтр НЧ — второй, то лишние детали из приведённой выше схемы (то есть один конденсатор и одну катушку) надо убирать непременно с «хвоста» схемы, а не наоборот. Иначе вы получите несколько неожиданные эффекты от изменения характера нагружения предыдущих каскадов фильтра.
Мы не успели познакомиться с эллиптическими фильтрами. Ну, значит, в следующий раз с них и начнём.
Подготовлено по материалам журнала "Автозвук", май 2009 г. www.avtozvuk.com
То есть очень даже не совсем. Дело в том, что схематика пассивных фильтров довольно разнообразна. Мы сразу открестились от фильтров с нормирующим резистором на входе, поскольку в акустике они почти не применяются, если, конечно, не считать тех случаев, когда головку (пищалку или среднечастотник) надо «осадить» ровно на 6 дБ. Почему на шесть? Потому что в таких фильтрах (они ещё называются двунагруженными) номинал входного резистора выбирается таким же, как импеданс нагрузки, скажем, 4 Ом, и в полосе пропускания такой фильтр будет давать аттенюацию на 6 дБ. К тому же двунагруженные фильтры бывают П-типа и Т-типа. Чтобы представить себе фильтр П-типа, достаточно отбросить первый элемент (Z1) на схеме обобщённого фильтра (рис. 20, №5/2009). Первый элемент такого фильтра включён в землю, и если входного резистора в схеме фильтра нет (однонагруженный фильтр), то этот элемент не создаёт фильтрующего эффекта, а лишь нагружает источник сигнала. (Попробуйте источник, то есть усилитель, включить на конденсатор в несколько сотен микрофарад, а потом напишите мне — успела у него сработать защита или нет. На всякий случай пишите до востребования, дающим такие советы адресами лучше не сорить.) Поэтому П-фильтры мы тоже не рассматриваем. Итого, как нетрудно представить, мы имеем дело с одной четвёртой из схемных реализаций пассивных фильтров.
Эллиптические фильтры стоят особняком, потому хотя бы, что у них лишний элемент и лишний корень полиномиального уравнения. Мало того, корни этого уравнения распределены в комплексной плоскости не по кругу (как у Баттерворта, скажем), а по эллипсу. Чтобы не оперировать понятиями, прояснять которые здесь, наверное, нет смысла, эллиптические фильтры мы будем называть (как и все прочие) по имени учёного, которые описал их свойства. Итак…
Схемы фильтров Кауэра
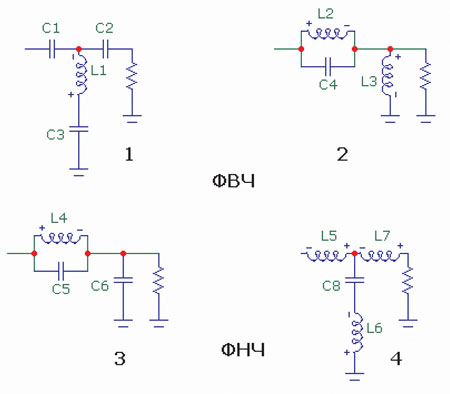
Известно по две схемные реализации фильтров Кауэра — для ФВЧ и ФНЧ (рис. 1).
Те, которые обозначены у меня нечётными номерами, называются стандартными, две другие — дуальными. Почему так, а не иначе? Может, потому, что в стандартных схемах дополнительным элементом является ёмкость, а дуальные схемы отличаются от обычного фильтра присутствием дополнительной индуктивности. Кстати говоря, далеко не всякая схема, полученная таким способом, является эллиптическим фильтром, если всё делать по науке, надо строго соблюдать соотношения между элементами.
Фильтр Кауэра имеет изрядное количество недостатков О них, как всегда, во вторую очередь, давайте мыслить позитивно. Ведь есть у Кауэра плюс, который в иных случаях способен всё перевесить. Такой фильтр обеспечивает глубокое подавление сигнала на частоте настройки резонансной цепи (L1-C3, L2-C4, L4-C5, L6-C8 на схемах 1 — 4). В частности, если требуется обеспечить фильтрацию вблизи частоты резонанса головки, то с такой задачей только фильтры Кауэра и справляются. Вручную считать их довольно хлопотно, однако в программах-симуляторах существуют, как правило, специальные разделы, посвящённые пассивным фильтрам. Правда, не факт, что там найдутся однонагруженные фильтры. Впрочем, по моему мнению, не будет большого вреда, если вы возьмёте схему фильтра Чебышёва или Баттерворта, а дополнительный элемент рассчитаете по частоте резонанса по известной формуле:
Fр = 1/(2 ? (LC)^1/2), откуда
C = 1/(4 ? ^2 Fр ^2 L) (3.1)
Обязательное условие: резонансная частота должна находиться вне полосы прозрачности фильтра, то есть для фильтра ВЧ — ниже частоты среза, для фильтра НЧ — выше частоты среза «исходного» фильтра. С практической точки зрения наибольший интерес представляют собой фильтры ВЧ этого типа — случается, что полосу среднечастотника или пищалки желательно ограничить как можно ниже, исключая, однако, её работу вблизи частоты резонанса головки. Для унификации я привожу схему фильтра ВЧ для любимой нами частоты 100 Гц (рис. 2).
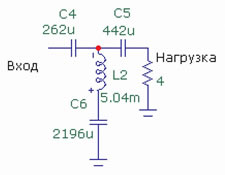
Номиналы элементов выглядят несколько диковато (особенно ёмкость 2196 мкФ — частота резонанса 48 Гц), но как только вы перейдёте к более высоким частотам, то и номиналы изменятся обратно пропорционально квадрату частоты, то есть — быстро.
Типы фильтров, плюсы и минусы
Как уже было сказано, характеристики фильтров определяются неким полиномом (многочленом) соответствующего порядка. Поскольку в математике описано энное количество специальных категорий полиномов, то и типов фильтров может быть ровно столько же. Даже на самом деле ещё больше, поскольку в акустике тоже было принято давать некоторым категориям фильтров специальные названия. Коль скоро существуют полиномы Баттерворта, Лежандра, Гаусса, Чебышёва (совет: пишите и произносите фамилию Пафнутия Львовича через «ё», как это положено — это самый лёгкий способ показать основательность собственного образования), Бесселя и проч., то существуют и фильтры, носящие все эти фамилии. К тому же полиномы Бесселя изучали с перерывами чуть ли не сто лет, поэтому их самих, как и соответствующие фильтры, немец назовёт по имени своего соотечественника, а англичанин, скорее всего, вспомнит Томсона. Особая статья — фильтры Линквица. Их автор (живёхонький и бодрый) предложил некую категорию фильтров ВЧ и НЧ, сумма выходных напряжений которых давала бы ровную частотную зависимость. Дело вот в чём: если в точке раздела спад выходного напряжения каждого фильтра составляет 3 дБ, то по мощности (квадрату напряжения) суммарная характеристика будет прямолинейна, а по напряжению в точке сопряжения появится горб 3 дБ. Линквиц предложил сопрягать фильтры по уровню -6 дБ. В частности, фильтры Линквица второго порядка — это те же самые фильтры Баттерворта, только для фильтра ВЧ у них выбирается частота среза в 1,414 раза выше, чем для фильтра НЧ. (Частота сопряжения находится точно между ними, то есть в 1,189 раза выше, чем у ФНЧ Баттерворта с теми же номиналами.) Поэтому когда мне встречается усилитель, в котором перестраиваемые фильтры специфицируются как фильтры Линквица, я понимаю, что авторы разработки и составители спецификации не были друг с другом знакомы. Впрочем, вернёмся к событиям 25 — 30-летней давности. Во всеобщем торжестве фильтростроения поучаствовал и Рихард Смолл, который предложил фильтры Линквица объединить (для удобства, не иначе) с последовательными фильтрами, которые тоже обеспечивают ровную характеристику по напряжению, и назвать всё вместе фильтрами постоянного напряжения (constant voltage design). Это притом что ни тогда, ни, кажется, и теперь, толком не установлено, является ли предпочтительной ровная характеристика по напряжению или же по мощности. Один из авторов даже вычислил промежуточные полиномиальные коэффициенты, так что фильтры, соответствующие этим «компромиссным» полиномам, должны были дать в точке сопряжения 1,5-децибельный горб по напряжению и такой же величины провал по мощности. Одним из дополнительных требований к конструкциям фильтров являлось то, что фазочастотные характеристики фильтров НЧ и ВЧ должны быть либо идентичными, либо расходиться на 180 градусов — а значит, при перемене полярности включения одного из звеньев будет опять же получена идентичная фазовая характеристика. В результате, кроме всего прочего, удаётся минимизировать область перехлёста полос.
Возможно, что все эти игры разума оказались очень кстати в разработках многополосных компрессоров, экспандеров и иных процессорных систем. Вот только в акустике применить их, мягко говоря, затруднительно. Во-первых, складываются не напряжения, а звуковые давления, которые связаны с напряжением через хитрую фазочастотную характеристику (рис. 15, №5/2009), так что не только фазы у них могут произвольно различаться, но и крутизна фазовой зависимости наверняка будет разной (если только вам не пришло в голову разводить по полосам однотипные головки). Во-вторых, напряжение и мощность связаны со звуковым давлением и акустической мощностью через КПД головок, а они тоже не обязаны быть одинаковыми. Поэтому, как мне кажется, во главу угла надо ставить не сопряжение фильтров по полосам, а собственные характеристики фильтров.
Какие характеристики (с позиций акустики) определяют качество фильтров? Некоторые фильтры обеспечивают гладкую частотную характеристику в полосе прозрачности, у других же спад начинается задолго до достижения частоты среза, но и после неё крутизна спада медленно выходит на нужную величину, у третьих на подходе к частоте среза наблюдается горб («зубец»), после которого начинается резкий спад с крутизной даже несколько выше «номинала». С этих позиций качество фильтров характеризуется «гладкостью АЧХ» и «избирательностью». Перепад фаз для фильтра данного порядка величина фиксированная (об этом было в прошлом выпуске), но изменение фазы может быть либо постепенным, либо быстрым, сопровождающимся значительным ростом группового времени задержки. Это свойство фильтра характеризуется гладкостью фазы. Ну и качество переходного процесса, то есть реакция на ступенчатое воздействие (Step Response). Фильтр НЧ переход с уровня на уровень отрабатывает (правда, с задержкой), но процесс перехода может сопровождаться выбросом и колебательным процессом. У фильтра ВЧ реакция на ступеньку — это всегда острый пик (без задержки) с возвратом к нулевой постоянной составляющей, но переброс через ноль и последующие колебания похожи на то, что можно увидеть у фильтра НЧ того же типа.
На мой взгляд (моё мнение может быть небесспорным, желающие спорить могут вступить в переписку, даже не до востребования), для акустических целей вполне достаточно фильтров трёх типов: Баттерворта, Бесселя и Чебышёва, тем более что последний тип на самом деле объединяет целую группу фильтров с разной магнитудой «зубцов». По части гладкости АЧХ в полосе прозрачности вне конкуренции фильтры Баттерворта — их частотную характеристику так и называют характеристикой наибольшей гладкости. А дальше, если взять ряд Бессель — Баттерворт — Чебышёв, то в этом ряду идёт возрастание избирательности с одновременным убыванием гладкости фазы и качества переходного процесса (рис. 3, 4).
Хорошо видно, что частотная характеристика у Бесселя самая плавная, у Чебышёва — самая «решительная». Фазочастотная характеристика у фильтра Бесселя тоже самая плавная, у Чебышёва — самая «угловатая». Для общности привожу ещё характеристики фильтра Кауэра, схема которого была показана чуть выше (рис. 5).
Обратите внимание на то, как в точке резонанса (48 Гц, как и обещал) фаза скачком меняется на 180 градусов. Конечно, на этой частоте подавление сигнала должно быть наивысшим. Но в любом случае понятия «плавность фазы» и «фильтр Кауэра» никак не совмещаются.
Теперь посмотрим, как выглядит переходная характеристика фильтров четырёх типов (все — фильтры НЧ на частоту среза 100 Гц) (рис. 6).
Фильтр Бесселя, как и все прочие, имеет третий порядок, но у него практически нет выброса. Наибольшая величина выбросов у Чебышёва и Кауэра, причём у последнего колебательный процесс имеет большую протяжённость. Величина выброса растёт с ростом порядка фильтра и, соответственно, падает по мере его снижения. Для иллюстрации привожу переходные характеристики фильтров второго порядка Батерворта и Чебышёва (с Бесселем проблем не возникает) (рис. 7).
Кроме того, мне попалась табличка зависимости величины переброса от порядка фильтра Баттерворта, которую я тоже решил привести (таб. 1).
Это одна из причин, по которым вряд ли стоит увлекаться фильтрами Баттерворта порядка выше четвёртого и Чебышёва — выше третьего, как, впрочем, и фильтрами Кауэра. Отличительная особенность последнего — крайне высокая чувствительность к разбросу параметров элементов. По моему опыту, точность подбора деталей в процентах можно определить как 5/n, где n — порядок фильтра. То есть, работая с фильтром четвёртого порядка, вы должны быть готовы к тому, что номинал деталей придётся подбирать с точностью 1% (для Кауэра — 0,25%!).
И вот теперь настала пора перейти к выбору деталей. Электролитов, конечно, следует избегать из-за их нестабильности, хотя, если счёт емкостей идёт на сотни микрофарад, иного выхода нет. Ёмкости, конечно, придётся подбирать и набирать из нескольких конденсаторов. При желании можно найти электролиты с малыми утечками, малым сопротивлением выводов и реальным разбросом ёмкости не хуже +20/-0%. Катушки, понятно, лучше «бессердечные», если без сердечника никак, я предпочитаю ферриты.
Для подбора номиналов предлагаю воспользоваться следующей таблицей. Все фильтры рассчитаны на частоту среза 100 Гц (-3 дБ) и номинал нагрузки 4 Ом. Чтобы получить значения номиналов для вашего проекта, надо каждый из элементов пересчитать по нехитрым формулам:
A = At Zs 100/(4*Fc) (3.2),
где At — это соответствующее табличное значение, Zs — номинальный импеданс динамической головки, а Fc, как всегда — расчётная частота среза. Внимание: номиналы индуктивностей приведены в миллигенри (а не в генри), номиналы емкостей — в микрофарадах (а не в фарадах). Наукообразия меньше, удобства — больше (таб. 2).
Впереди у нас ещё одна интересная тема — частотная коррекция в пассивных фильтрах, но её мы рассмотрим на следующем занятии.
В прошлой главе серии мы в первом приближении познакомились со схемами пассивных фильтров. Правда, не совсем.
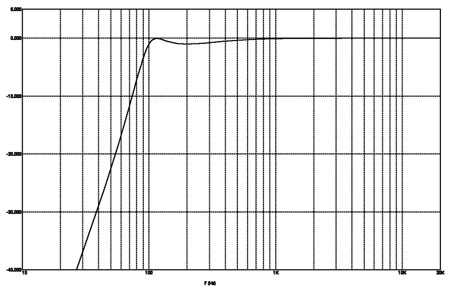
Рис. 3в
АЧХ Чебышёва третьего порядка
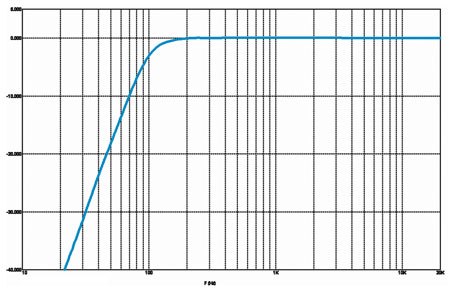
Рис. 3б
АЧХ Баттерворта третьего порядка
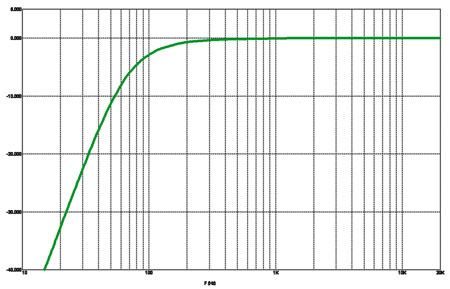
Рис. 3а
АЧХ Бесселя третьего порядка
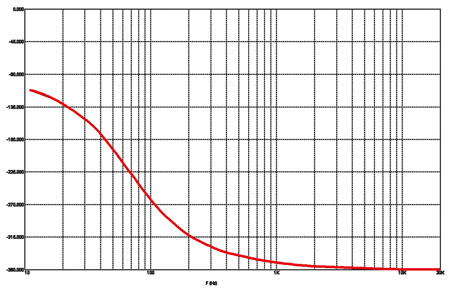
Рис. 4а
ФЧХ Бесселя третьего порядка
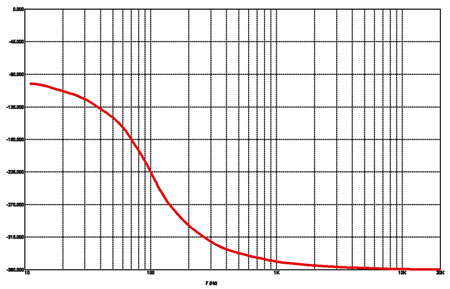
Рис. 4б
ФЧХ Баттерворта третьего порядка
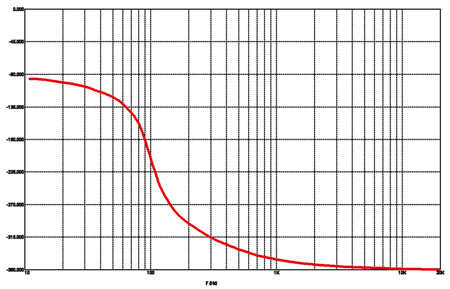
Рис. 4в
ФЧХ Чебышёва третьего порядка
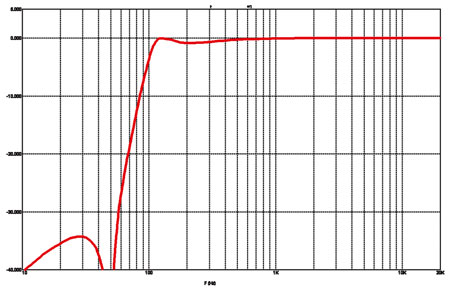
Рис. 5а
АЧХ фильтра Кауэра третьего порядка
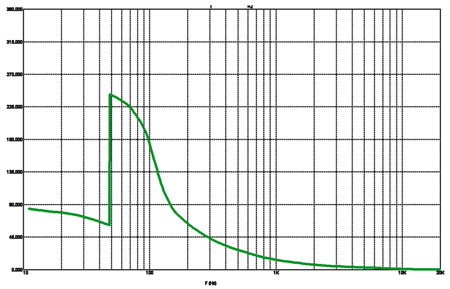
Рис. 5б
ФЧХ фильтра Кауэра третьего порядка
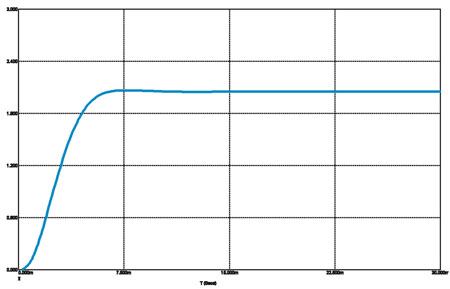
Рис. 6а
Переходная характеристика Бесселя
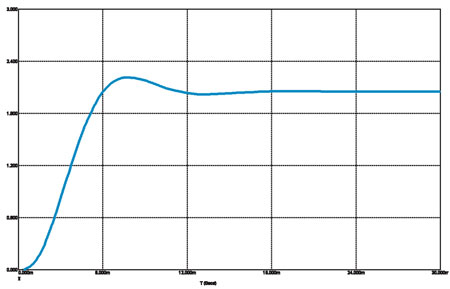
Рис. 6б
Переходная характеристика Баттерворта
|
Порядок фильтра |
2 |
3 |
4 |
5 |
|
Величина выброса, % |
4,3 |
8,15 |
10,9 |
12,8 |
|
Фильтр НЧ |
Фильтр ВЧ |
||||||||
|
Порядок фильтра |
L1 |
C1 |
L2 |
C2 |
C1 |
L1 |
C2 |
L2 |
|
|
Баттерворт |
1 |
6,365 |
397,6 |
||||||
|
2 |
9,000 |
281,16 |
281,16 |
9,000 |
|||||
|
3 |
9,545 |
529,55 |
3,180 |
265,78 |
4,775 |
795,4 |
|||
|
4 |
10,83 |
627,13 |
6,442 |
146,6 |
233,80 |
4,040 |
393,2 |
17,278 |
|
|
Линквиц |
2 |
12,725 |
198,87 |
198,87 |
12,725 |
||||
|
4 |
12,02 |
634,75 |
5,989 |
141,9 |
210,84 |
4,004 |
421,65 |
18,000 |
|
|
Бессель |
2 |
11,02 |
228,0 |
228,0 |
11,02 |
||||
|
3 |
9,370 |
336,0 |
1,850 |
279,0 |
8,000 |
1390,0 |
|||
|
4 |
14,33 |
584,0 |
5,850 |
126,0 |
175,5 |
3,450 |
179,75 |
19,930 |
|
|
Чебышёв |
2 |
7,963 |
497,5 |
497,5 |
7,963 |
||||
|
3 |
9,650 |
529,5 |
6,435 |
261,8 |
4,805 |
392,5 |
|||
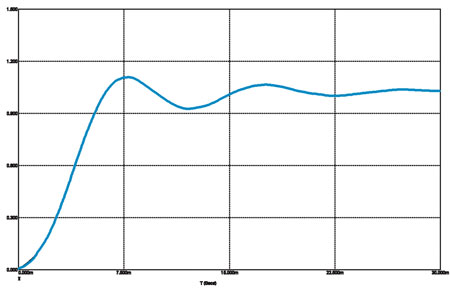
Рис. 6г
Переходная характеристика Кауэра
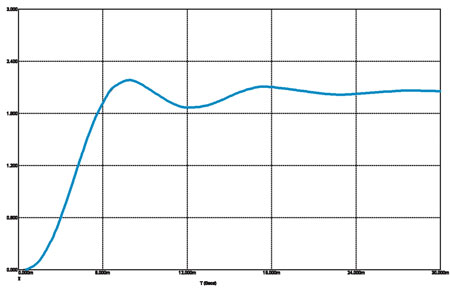
Рис. 6в
Переходная характеристика Чебышёва
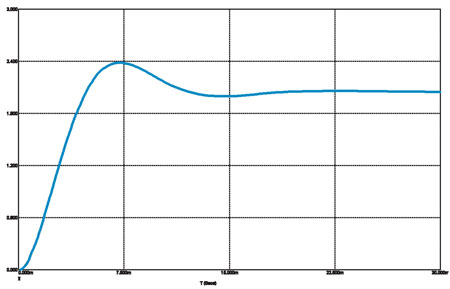
Рис. 7б
Переходная характеристика Чебышёва
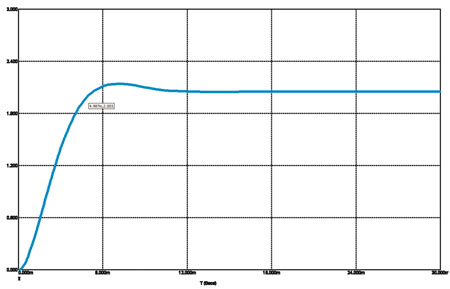
Рис. 7а
Переходная характеристика Баттерворта
Подготовлено по материалам журнала "Автозвук", июль 2009 г. www.avtozvuk.com
Устройства и цепи, входящие в состав пассивных фильтров (конечно, если это фильтры соответствующего уровня), можно разделить на три группы: аттенюаторы, устройства частотной коррекции и то, что англоговорящие граждане называют miscellaneous, попросту говоря, «разное».
Аттенюаторы
Поначалу это может показаться удивительным, но аттенюатор является непременным атрибутом многополосной акустики, ибо головки для разных полос не только не всегда имеют, но и не должны иметь одинаковую чувствительность. В противном случае свобода манёвра по частотной коррекции будет сведена к нулю. Дело в том, что в системе пассивной коррекции, чтобы исправить провал, надо «осадить» головку в основной полосе и «отпустить» там, где был провал. Кроме того, в жилых помещениях часто бывает желательно, чтобы пищалка немного «переигрывала» по громкости мидбас или среднечастотник и бас. В то же время «осаживать» басовый динамик выходит накладно в любом смысле — требуется целая группа мощных резисторов, и изрядная часть энергии усилителя уходит на разогрев упомянутой группы. На практике считается оптимальным, когда отдача среднечастотника на несколько (2 — 5) децибел выше, чем у баса, а у пищалки на столько же выше, чем у СЧ-головки. Так что без аттенюаторов не обойтись.
Как известно, электротехника оперирует комплексными величинами, а никак не децибелами, так что мы ими сегодня будем пользоваться лишь отчасти. Поэтому для вашего удобства привожу табличку пересчёта показателя аттенюации (дБ) в коэффициент пропускания устройства.
Итак, если вам нужно «осадить» головку на 4 дБ, коэффициент пропускания N аттенюатора должен быть равен 0,631. Простейший вариант — последовательный аттенюатор — как явствует из названия, устанавливается последовательно с нагрузкой. Если ZL — средний импеданс головки в области, представляющий интерес, то номинал RS последовательного аттенюатора определится по формуле:
RS = ZL * (1 - N)/N (4.1)
В качестве ZL можно брать «номинал» 4 Ом. Если мы из лучших побуждений установим последовательный аттенюатор прямо перед головкой (китайцы, как правило, так и делают), то импеданс нагрузки для фильтра увеличится, и частота среза НЧ возрастёт, а фильтра ВЧ — понизится. Но это ещё не все.
Берём для примера аттенюатор 3 дБ, работающий на 4 Ом. Номинал резистора по формуле (4,1) будет равен 1,66 Ом. На рис. 1 и 2 — то, что получится при использовании фильтра ВЧ на 100 Гц, а также фильтра НЧ на 4000 Гц.
Синие кривые на рис. 1 и 2 — частотные характеристики без аттенюатора, красные — АЧХ с последовательным аттенюатором, включённым после соответствующего фильтра. Зелёная кривая соответствует включению аттенюатора перед фильтром. Единственное побочное явление — смещение частоты на 10 — 15% в минус и в плюс для ФВЧ и ФНЧ соответственно. Так что в большинстве случаев последовательный аттенюатор должен устанавливаться перед фильтром.
Чтобы избежать дрейфа частоты среза при включении аттенюатора, были придуманы устройства, которые у нас называются Г-образные аттенюаторы, а в остальной части мира, где алфавит не содержит волшебной и такой нужной в повседневной жизни буквы «Г», носят название L-Pad. Такой аттенюатор состоит из двух резисторов, один из них, RS, включается последовательно с нагрузкой, второй, Rp — параллельно. Вычисляются они так:
RS = ZL * (1 - N), (4.2)
Rp = ZL * N/(1 - N) (4.3)
Для примера берём те же 3 дБ аттенюации. Номиналы резисторов получились такие, как показано на схеме (ZL опять же 4 Ом).
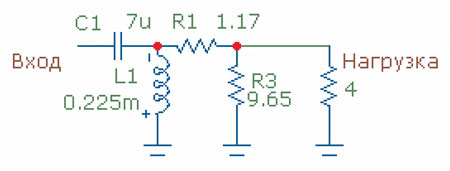
Рис. 3. Схема Г-образного аттенюатора
Здесь аттенюатор показан вместе с фильтром ВЧ на 4 кГц. (Для единообразия все фильтры сегодня — типа Баттерворта.) На рис. 4 вы видите обычный набор характеристик. Синяя кривая — без аттенюатора, красная — с аттенюатором, включённым до фильтра, и зелёная — с аттенюатором после фильтра.
Как видим, у красной кривой и добротность ниже, и частота среза смещена вниз (у фильтра НЧ она будет смещаться вверх на те же 10%). Так что не надо мудрить — L-Pad лучше включать именно так, как показано на предыдущем рисунке, непосредственно перед головкой. Впрочем, при определённых обстоятельствах перестановкой можно воспользоваться — не меняя номиналы, подкорректировать область раздела полос. Но это уже высший пилотаж… А теперь переходим к «разному».
Другие употребительные схемы
Чаще других в наших кроссоверах встречается цепь коррекции импеданса головки, обычно называемая цепью Цобеля по имени известного исследователя характеристики фильтров. Она представляет собой последовательную RC цепочку, включённую параллельно нагрузке. По классическим формулам
R = ZL (4.4),
C = Le/R2e (4.5), где
Le = [(Z2L - R2e)/2?pFo]1/2 (4.6).
Здесь ZL — импеданс нагрузки на частоте Fo, представляющей интерес. Как правило, за параметр ZL, не мудрствуя лукаво, выбирают номинальный импеданс головки, в нашем случае, 4 Ом. Я бы советовал величину R искать по такой формуле:
R = k * Re (4.4a).
Здесь коэффициент k = 1,2 — 1,3, всё равно более точно резисторы не подобрать.
На рис. 5 вы можете видеть четыре частотные характеристики. Синяя — обычная характеристика фильтра Баттерворта, нагруженного на резистор 4 Ом. Красная кривая — такая характеристика получается, если звуковую катушку представить как последовательное соединение резистора 3,3 Ом и индуктивности 0,25 мГн (такие параметры характерны для сравнительно лёгкого мидбаса). Почувствуйте разницу, как говорится. Чёрным цветом показано, как будет выглядеть АЧХ фильтра, если разработчик не станет упрощать себе жизнь, а параметры фильтра определит по формулам 4.4 — 4.6, исходя из полного импеданса катушки — при указанных параметрах катушки полный импеданс составит 7,10 Ом (4 кГц). Наконец, зелёная кривая — это АЧХ, полученная с использованием цепи Цобеля, элементы которой определены по формулам (4.4а) и (4.5). Расхождение зелёной и синей кривых не превышает 0,6 дБ в диапазоне частот 0,4 — 0,5 от частоты среза (в нашем примере это 4 кГц). На рис. 6 вы видите схему соответствующего фильтра с «Цобелем».
Кстати говоря, когда в кроссовере вы находите резистор номиналом 3,9 Ом (реже — 3,6 или 4,2 Ом), можно с минимальной вероятностью ошибки утверждать, что в схеме фильтра задействована цепочка Цобеля. Но есть и другие схемные решения, приводящие к появлению «лишнего» элемента в схеме фильтра.
Конечно, я имею в виду так называемые «странные» фильтры (Strange Filters), которые отличаются наличием дополнительного резистора в земляной цепи фильтра. Уже хорошо нам известный фильтр НЧ на 4 кГц можно представить в таком виде (рис. 7).
Резистор R1 с номиналом 0,01 Ом можно рассматривать как сопротивление выводов конденсатора и соединяющих дорожек. А вот если номинал резистора становится существенным (то есть сравнимым с номиналом нагрузки), получится «странный» фильтр. Будем менять резистор R1 в диапазоне от 0,01 до 4,01 Ом с шагом 1 Ом. Полученное семейство частотных характеристик можно увидеть на рис. 8.
Верхняя кривая (в области точки перегиба) — обычная баттервортовская характеристика. По мере роста номинала резистора частота среза фильтра сдвигается вниз (до 3 кГц при R1 = 4 Ом). Но крутизна спада меняется незначительно, по крайней мере в пределах полосы, ограниченной уровнем -15 дБ — а именно эта область имеет практическое значение. Ниже этого уровня крутизна спада будет стремиться к 6 дБ/окт., но это не так уж и важно. (Обратите внимание, масштаб графика по вертикали изменён, поэтому спад кажется более крутым.) А теперь посмотрим, как меняется фазочастотная характеристика в зависимости от номинала резистора (рис. 9).
Характер поведения графика ФЧХ изменяется начиная с 6 кГц (то есть от 1,5 частот среза). С использованием «странного» фильтра можно плавно регулировать взаимную фазу излучения соседних головок, чтобы добиться желаемой формы общей частотной характеристики.
Теперь в соответствии с законами жанра прервёмся, пообещав, что в следующий раз будет ещё интереснее.
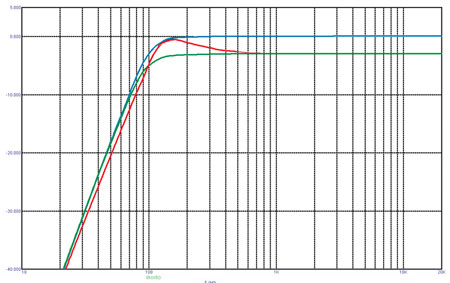
Рис. 1. АЧХ последовательного аттенюатора (ФВЧ)
|
Аттенюация, дБ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Коэффициент пропускания |
0,891 |
0,794 |
0,707 |
0,631 |
0,562 |
0,501 |
0,447 |
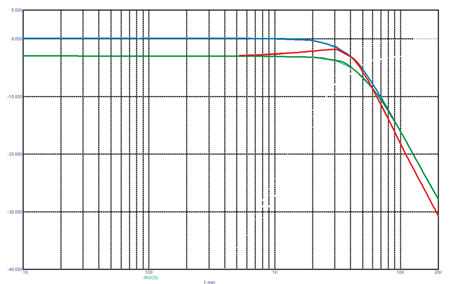
Рис. 2. То же для ФНЧ
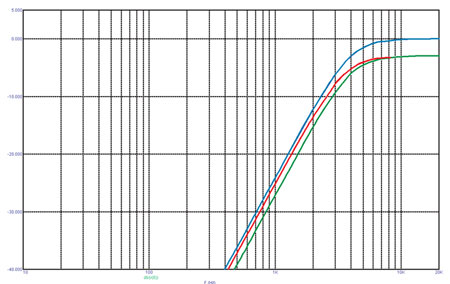
Рис. 4. Частотные характеристики Г-образного аттенюатора
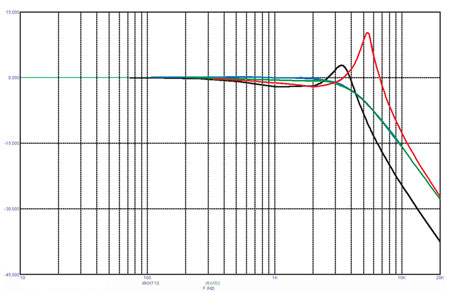
Рис. 5. Частотные характеристики фильтра со схемой Цобеля
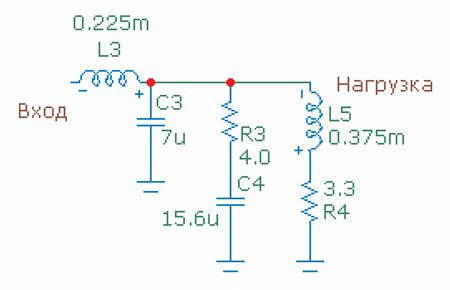
Рис. 6. Схема фильтра с цепью Цобеля
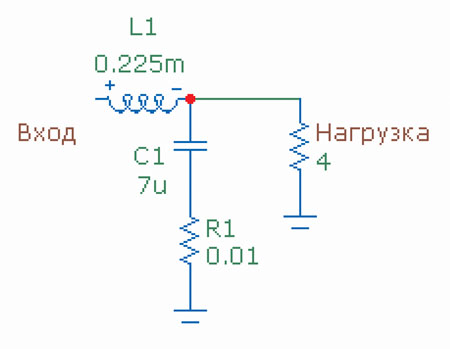
Рис. 7. Схема «странного» фильтра
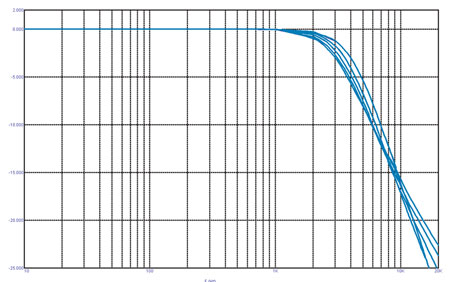
Рис. 8. Амплитудно-частотные характеристики «странного» фильтра
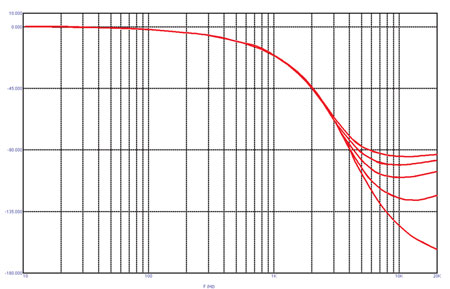
Рис. 9. Фазочастотные характеристики «странного» фильтра
Подготовлено по материалам журнала "Автозвук", август 2009 г. www.avtozvuk.com
Как и было обещано, сегодня наконец вплотную займёмся схемами частотной коррекции.
В своих трудах я не раз и не два утверждал, что пассивные фильтры могут многое такое, что активным фильтрам не под силу. Утверждал огульно, ничем свою правоту не доказывая и ничего не поясняя. А действительно, чего же не могут активные фильтры? Свою основную задачу — «отсекать лишнее» — они решают вполне успешно. И хотя именно в силу своей универсальности активные фильтры, как правило, имеют баттервортовские характеристики (если они вообще выполнены правильно), но фильтры Баттерворта, как вы уже, надеюсь, поняли, в большинстве случаев представляют собой оптимальный компромисс между формой амплитудно- и фазочастотной характеристики, а также качеством переходного процесса. А возможность плавной перестройки частоты вообще слишком многое компенсирует. По части согласования уровней активные системы, безусловно, переигрывают любые аттенюаторы. И есть лишь единственная статья, по которой активные фильтры проигрывают — частотная коррекция.
В ряде случаев может быть полезен параметрический эквалайзер. Но у аналоговых эквалайзеров часто не хватает либо диапазона изменения частоты, либо пределов перестройки добротности, либо того и другого. У многополосных параметриков, как правило, того и другого с запасом, но они добавляют в тракт шумов. К тому же это игрушки дорогие и в нашей отрасли — редкость. Цифровые параметрические эквалайзеры подходят идеально, если у них шаг перестройки центральной частоты 1/12 октавы, а такие у нас тоже, кажется, не водятся. Параметрики с шагом 1/6 октавы подходят частично и при условии, что у них достаточно широкий набор доступных значений добротности. Вот и получается, что лишь пассивные корректирующие устройства в наибольшей мере соответствуют поставленным задачам. Кстати, студийные мониторы высокого качества часто так и делают: би-ампинг/три-ампинг с активной фильтрацией и пассивными корректирующими устройствами.
Верхнечастотная коррекция
На верхних частотах, как правило, требуется подъём АЧХ, опускается она сама и без всяких корректоров. Цепочка, состоящая из параллельно соединённых конденсатора и резистора, называется ещё рупорным контуром (поскольку в рупорных излучателях без неё обходятся очень редко), а в современной (не нашей) литературе её часто именуют просто контуром (contour). Естественно, чтобы в пассивной системе поднять АЧХ на каком-то участке, надо вначале её опустить на всех остальных. Номинал резистора выбирается по обычной формуле для последовательного аттенюатора, которая была приведена в прошлой серии. Для удобства я её всё же приведу ещё раз:
RS = ZL (1 — N)/N (4.1)
Здесь, как и всегда, N — коэффициент пропускания аттенюатора, ZL — импеданс нагрузки.
Номинал конденсатора я выбираю по формуле:
C = 1/(2 ? F05 RS), (5.1)
где F05 — частота, на которой действие аттенюатора требуется «ополовинить».
Никто не запретит вам включить последовательно более одного «контура», чтобы избежать «насыщения» на частотной характеристике (рис. 1).
Для примера я взял тот же фильтр ВЧ Баттерворта второго порядка, для которого в прошлой главе мы определили номинал резистора Rs = 1,65 Ом для аттенюации на 3 дБ (рис. 2).
Такой двойной контур позволяет поднять «хвост» АЧХ (20 кГц) на 2 дБ.
Наверное, полезно будет напомнить, что умножение числа элементов умножает и ошибки из-за неопределённости характеристики импеданса нагрузки и разброса номиналов элементов. Так что связываться с трёх- и более ступенчатыми контурами я бы не советовал.
Подавитель пиков на АЧХ
В зарубежной литературе эту корректирующую цепочку называют peak stopper network или просто stopper network. Она состоит уже из трёх элементов — параллельно включённых конденсатора, катушки и резистора. Вроде усложнение небольшое, однако формулы расчёта параметров такой цепи получаются заметно более громоздкими.
Величина Rs определяется по той же формуле для последовательного аттенюатора, в которой мы на этот раз изменим одно из обозначений:
RS = ZL (1 — N0)/N0 (5.2).
Здесь N0 — коэффициент передачи цепи на центральной частоте пика. Скажем, если высота пика 4 дБ, то коэффициент передачи 0,631 (см. таблицу из прошлой главы). Обозначим как Y0 величину реактивного сопротивления катушки и конденсатора на частоте резонанса F0, то есть на той частоте, куда приходится центр пика на АЧХ динамика, который нам требуется подавить. Если Y0 нам известна, то значения ёмкости и индуктивности определятся по известным формулам:
C = 1/(2 ? F0 x Y0) (5.3)
L = Y0 /(2 ? F0) (5.4).
Теперь надо задаться ещё двумя значениями частот FL и FH — снизу и сверху от центральной частоты, где коэффициент передачи имеет значение N. N > N0, скажем, если N0 была задана как 0,631, параметр N может быть равным 0,75 или 0,8. Конкретное значение N определяется по графику АЧХ конкретного динамика. Ещё одна тонкость касается выбора значений FH и FL. Коль скоро корректирующая цепь в теории имеет симметричную форму АЧХ, то выбранные значения должны удовлетворять условие:
(FH x FL)1/2 = F0 (5.5).
Теперь наконец у нас есть все данные, чтобы определить параметр Y0.
Y0 = (FH — FL)/F0 sqr (1/(N2/(1 — N)2/ZL2 — 1/R2)) (5.6).
Формула выглядит страшновато, но я же предупреждал. Пусть вас ободрит информация о том, что более громоздкие выражения нам уже не встретятся. Множитель перед радикалом — это относительная ширина полосы корректирующего устройства, то есть величина, обратно пропорциональная добротности. Чем добротность выше, тем (при той же центральной частоте F0) индуктивность будет меньше, а ёмкость больше. А потому при высокой добротности пиков возникает двойная «засада»: с ростом центральной частоты индуктивность становится слишком малой, и её трудно бывает изготовить с подобающим допуском (±5%); по мере уменьшения частоты потребная величина ёмкости возрастает до таких значений, что приходится «параллелить» энное количество конденсаторов.
В качестве примера рассчитаем схему корректора с такими параметрами. F0 = 1000 Гц, FH = 1100 Гц, FL = 910 Гц, N0 = 0,631, N = 0,794. Вот что получится (рис. 3).
А вот как будет выглядеть АЧХ нашей цепи (рис. 4). При нагрузке чисто резистивного характера (синяя кривая) мы получаем почти в точности то, на что и рассчитывали. В присутствии индуктивности головки (красная кривая) корректирующая АЧХ становится несимметричной.
Характеристики такого корректора мало зависят от того, поставлен он до или после фильтра ВЧ или фильтра НЧ. На следующих двух графиках (рис. 5 и 6) красная кривая соответствует включению корректора до соответствующего фильтра, синяя — включению его после фильтра.
Схема компенсации провала на АЧХ
То, что было сказано в отношении высокочастотного корректирующего контура, относится и к схеме компенсации провала: чтобы на каком-то участке поднять АЧХ, требуется вначале опустить её на всех прочих. Схема состоит из тех же трёх элементов Rs, L и C, с той только разницей, что реактивные элементы включаются последовательно. На частоте резонанса они шунтируют резистор, который за пределами зоны резонанса действует как последовательный аттенюатор.
Подход к определению параметров элементов точно такой же, как и в случае с подавителем пиков. Мы должны знать центральную частоту F0, а также коэффициенты пропускания N0 и N. В данном случае N0 имеет смысл коэффициента пропускания цепи вне области коррекции (N0, как и N, меньше единицы). N суть коэффициент пропускания в точках АЧХ, соответствующих частотам FH и FL. Значения частот FH, FL должны отвечать тому же условию, то есть, если на реальной АЧХ головки вы видите несимметричный провал, для этих частот вы должны выбрать компромиссные значения, чтобы условие (5.5) примерно соблюдалось. Кстати, хотя нигде это явно не сказано, но наиболее практично выбирать уровень N таким образом, чтобы его значение в децибелах соответствовало половине от уровня N0. Именно так мы поступили в примере предыдущего раздела, N0 и N соответствовали уровни -4 и -2 дБ.
Номинал резистора определится по той же формуле (5.2). Значения ёмкости C и индуктивности L будут связаны с величиной реактивного импеданса Y0 на частоте резонанса F0 теми же зависимостями (5.3), (5.4). И лишь формула для расчёта Y0 будет несколько отличаться:
Y0 = F0/(FH-FL) sqr (1/(N2/(1 — N)2/ZL2 — 1/R2)) (5.7).
Как и было обещано, эта формула ничуть не более громоздкая, нежели равенство (5.6). Мало того, (5.7) от (5.6) отличается обратной величиной множителя перед выражением для корня. То есть с ростом добротности характеристики корректирующей цепи возрастает Y0, а значит, растёт величина потребной индуктивности L и падает величина ёмкости C. В этой связи проблема появляется лишь одна: при достаточно низкой центральной частоте F0 требуемая величина индуктивности заставляет использовать катушки с сердечниками, а там возникают свои проблемы, останавливаться на которых здесь, наверное, нет смысла.
Для примера берём цепь с точно такими же параметрами, как и для схемы подавителя пика. Именно: F0 = 1000 Гц, FH = 1100 Гц, FL = 910 Гц, N0 = 0,631, N = 0,794. Номиналы получаются такие, как показаны на схеме (рис. 7).
Обратите внимание, что величина индуктивности катушки здесь чуть ли не в двадцать раз больше, чем для схемы подавителя пиков, а ёмкость во столько же раз меньше. АЧХ рассчитанной нами схемы (рис. 8).
В присутствии индуктивности нагрузки (0,25 мГн) эффективность последовательного аттенюатора (резистора Rs) с ростом частоты падает (красная кривая), и появляется подъём на высоких частотах.
Цепь компенсации провала можно ставить как с той, так и с другой стороны от фильтра (рис. 9 и 10). Но надо помнить, что, когда компенсатор установлен после фильтра ВЧ или НЧ (синяя кривая на рис. 9 и 10), добротность фильтра увеличивается и возрастает частота среза. Так, в случае с фильтром ВЧ частота среза переместилась с 4 до 5 кГц, а частота среза фильтра НЧ снизилась с 250 до 185 Гц.
На этом сериал, посвящённый пассивным фильтрам будем считать законченным. Конечно, многие вопросы остались «за бортом» нашего исследования, но, в конце концов, у нас общетехнический, а не научный журнал. И, по лично моему мнению, информации, приведённой в пределах серии, будет достаточно для решения большинства практических задач. Для тех, кто хотел бы получить дополнительные сведения, будет полезно обратиться к следующим ресурсам. Первый: http://www.educypedia.be/electronics/electronicaopening.htm. Это образовательный сайт, он выводит на другие сайты, посвящённые конкретным вопросам. В частности, много чего полезного по фильтрам (активным и пассивным, с программами расчёта) можно найти здесь: http://sim.okawa-denshi.jp/en/. Вообще, этот ресурс будет полезен тем, кто решил заняться инженерной деятельностью. Говорят, такие сейчас появляются...
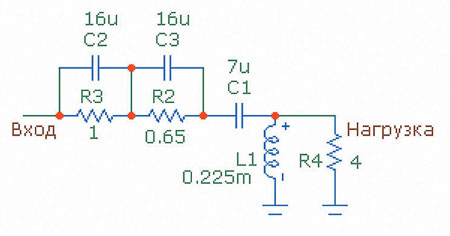
Рис. 1. Схема двойного ВЧ-контура
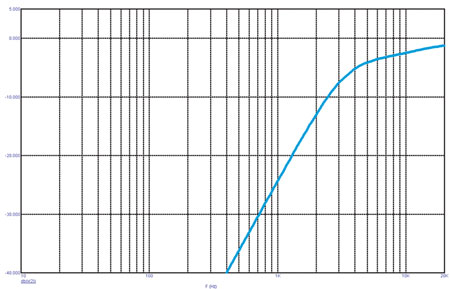
Рис. 2. АЧХ двойного корректирующего контура
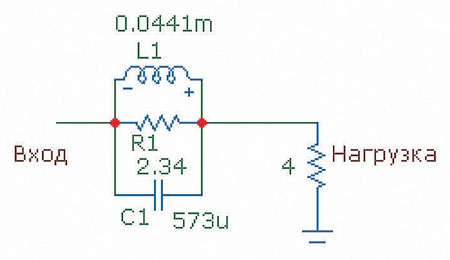
Рис. 3. Схема подавителя пика
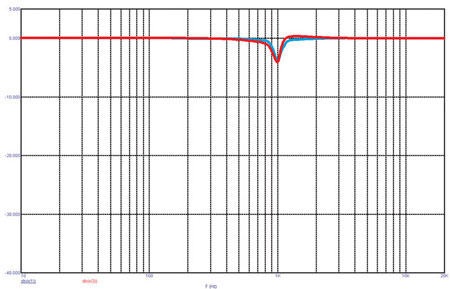
Рис. 4. Частотные характеристики схемы подавления пика
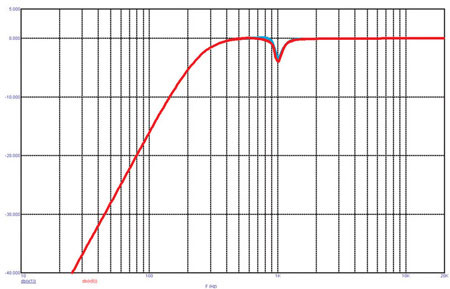
Рис. 5. Частотные характеристики корректора совместно с фильтром ВЧ
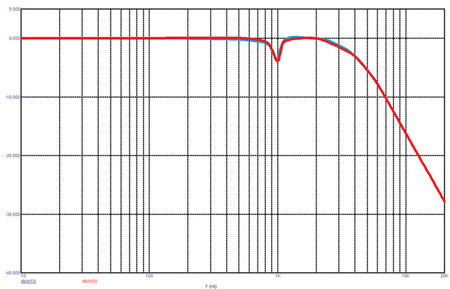
Рис. 6. Частотные характеристики корректора совместно с фильтром НЧ
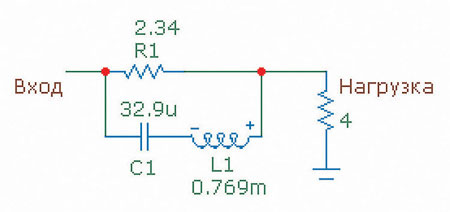
Рис. 7. Схема компенсации провала
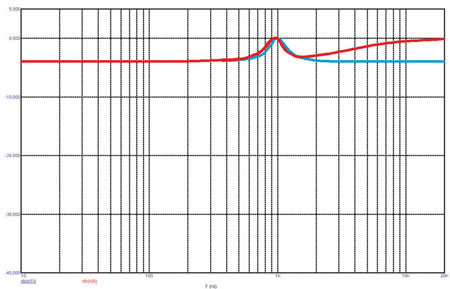
Рис. 8. Частотные характеристики схемы компенсации провала
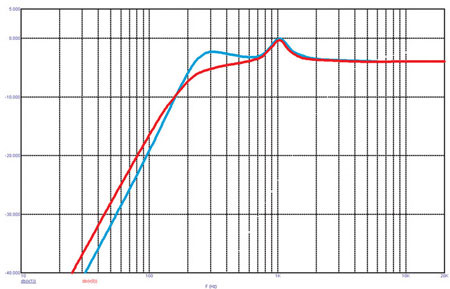
Рис. 9. Частотные характеристики цепи совместно с фильтром ВЧ
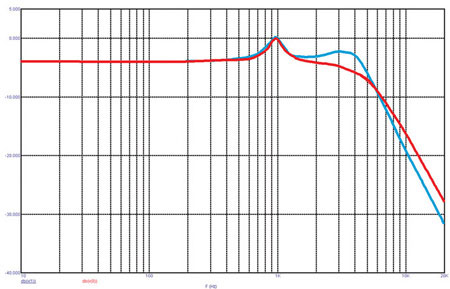
Рис. 10. Частотные характеристики цепи совместно с фильтром НЧ
Подготовлено по материалам журнала "Автозвук", октябрь 2009 г. www.avtozvuk.com









Опубликованная статья ставит своей целью "помочь разобраться с электрическими фильтрами". Высказывается мнение автора статьи. Только.
Wem/